最大异或后缀问题 Maximum Xor Suffix

之前在某公司OA碰上这问题了，当时也想了好久才整出解决方法，避免以后要用到就在这记录一下。其实这题的解法我交卷之后搜了搜也有，但大部分都只有个代码不带说明，或许附带说明可以更容易让人理解（当然也可能是高手们觉得一眼就能看懂没必要说明）。

问题简述

这问题英文叫Maxium Xor Suffix。简单来讲，输入为一个非空任意长度的整数数组，记为\([x_0, x_1, ..., x_n]\)，对此数组执行任意次（包括零次）此操作：选定一个有效数组下标\(i\)，计算 \(x_i \oplus x_{i+1} \oplus \dots \oplus x_n\)（\(\oplus\) 为位异或操作），并把执行结果附加在数组最后以形成新的数组。求数组最后一个元素能达到的最大值。

问题分析

因为以前没做过相关的题，一开始看到这题是挺头大的，但后面发现了这题的规律。

假设最初的数组有5个元素，设为\(A = [x_0, x_1, x_2, x_3, x_4]\)。假如我\(i\)选择4，那么新添加的元素就为\(x_4\)；假如选择3，就会是\(x_3 \oplus x_4\)，以此类推。于是，我把\(i\)为0到4时会添加到数组的元素设定为\(B = [y_0, y_1, y_2, y_3, y_4]\)（其中\(y_0 = x_0 \oplus \dots \oplus x_4\) ，直到\(y_4 = x_4\)）。最后添加到数组后面的元素必定为这五个其中之一。

假如我选了\(i = 0\)然后添加\(y_0\)到\(A\)里面，新的数组会变成\(A' = [x_0, x_1, x_2, x_3, x_4, y_0]\)。那么需要如何更新\(B\)呢？答案是\(B' = [y_0 \oplus y_0, y_1 \oplus y_0, y_2 \oplus y_0, y_3 \oplus y_0, y_4 \oplus y_0, y_0]\)。这其实并不难以理解，因为无论\(i\)为任意0~4的数字，每个\(y\)都会与新加入\(A\)的元素（因为它在最后一个）进行异或计算，然后这个新加入的元素刚好就是\(B[i] = y_i\)。比如当\(i = 0\)时， \(B'[1] = x1 \oplus x2 \oplus x3 \oplus x4 \oplus y_0 = y_1 \oplus y_0\)。

那假如我再进行一次操作呢？比方说，我这次选择\(i = 2\)。那添加到数组末尾的元素就会是 \(B'[2] = y_2 \oplus y_0\)。新的数组会变成 \(A'' = [x_0, x_1, x_2, x_3, x_4, y_0, y_2 \oplus y_0]\)。同样的，每个 \(B'\) 里的元素会被\(y_2 \oplus y_0\)所异或，变成\(B'' = [0 \oplus y_2 \oplus y_0, y_1 \oplus y_0 \oplus y_2 \oplus y_0, y_2 \oplus y_0 \oplus y_2 \oplus y_0, y_3 \oplus y_0 \oplus y_2 \oplus y_0, y_4 \oplus y_0 \oplus y_2 \oplus y_0] = [y_2 \oplus y_0, y_1 \oplus y_2, y_2 \oplus y_2, y_3 \oplus y_2, y_4 \oplus y_2]\)。原本在第一次操作中异或了\(y_0\)的元素这回异或\(y_2 \oplus y_0\)时，两个\(y_0\)相互抵消了，所以实际上变成了每个元素只与\(y_2\)异或。同理，\(B''[2] = 0\)，因为两次异或完全抵消了。

到这里就能发现最后一个元素的规律了。无论进行多少次操作，无论每一次操作选的\(i\)是多少，最终最后一个元素要不就是\(y_0\)到\(y_4\)中的一个，要不就是这五个数其中挑两个的异或和。现在问题就降级为了：

给定一个数组\(A\)
根据上面规则生成数组\(B\)（\(y_i = x_i \oplus x_{i+1} \oplus \dots \oplus x_n\)）
生成集合\(C\)，\(C = B \cup \{y_i \oplus y_j | y_i, y_j \in B\}\)
求集合\(C\)里最大的元素

找最大异或和

到了这一步，这个问题变成了Leetcode 421。如果先生成上面所述的集合再去找最大元素，会很慢（生成集合本身需要\(O(N^2)\)的时间）。最优解是使用字典树找出数组\(B\)里任意两个元素的最大异或和，然后再与其中最大元素做比较，得出最终结果。这样子使用的是\(O(N)\)的时间复杂度。

对于这道题，我们的字典树只需要两个分支，就跟二叉树一样。一个分支代表二进制0，一个分支代表二进制1。题目用的是 int ，因此这个搜索树有32层，顶部（根部）从每个数字的高位开始。

下面的样例可以使用这个网站进行可视化（把那一串二进制数字拷贝进去就行）：‌‌
https://cmps-people.ok.ubc.ca/ylucet/DS/Trie.html
不过因为比较长，需要调节一下画布大小

比如一个数组元素 12345 ，转换成二进制为 00000000000000000011000000111001 ，我们把它按照从左到右的顺序插入字典树。同样，我们可以插入 45678 、 56789 等（记得靠右对齐至32位）。这是插入的结果（只显示了分叉的位置）：

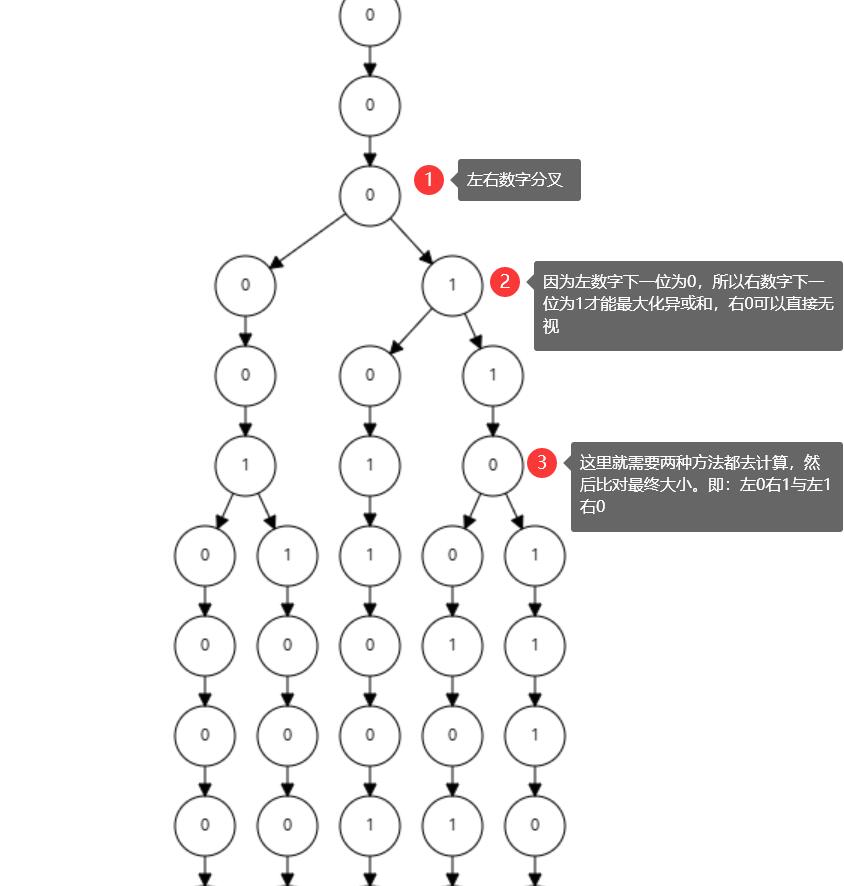
如上图，我们可以使用两个指针从上到下遍历。只有一个简单的规则： 如果有的选，左右两个指针选择不一样的位，即左1右0或者左0右1。只要遵循这个规则，最后出来的左右指针分别指向的最终数字的异或和一定是最大的（因为当两个数字进行位异或的时候，同样的两位会消掉）。

考虑到有可能会同时计算多种情况（即左右指针均有两种选择），建议使用递归来计算（函数可以接受左右指针作为参数，返回最后的异或和，在分叉的地方取两种情况的最大值，初始左右指针均为根节点）。同时，作为一种优化，字典树的叶节点可以存这个叶节点代表的数字，那就不需要再去把路径上的二进制位转换为十进制。

这样只需要\(O(N)\)时间建立字典树，以及静态时间进行查询（因为字典树高度固定）。

代码

这是用于Leetcode 421的代码。如果是用于最大异或后缀这道题，只需要把输入数组替换为\(B\)，然后最后在跟\(B\)内最大元素比较一下就行。如果原数组里有负数，那就还需要查最高位（下面代码忽略了最高位）。

// 2^0 to 2^30
// i.e. 00000000 00000000 00000000 00000001 to
//      01000000 00000000 00000000 00000000
// Highest bit is ignored because all numbers are non-negative
int divider[31] = {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096,
                    8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576,
                    2097152, 4194304, 8388608, 16777216, 33554432, 67108864,
                    134217728, 268435456, 536870912, 1073741824};

typedef struct TrieNode {
    // Pointer for 0 and 1
    struct TrieNode * next[2];
    // For leaf node only, representing the full number
    int number;
} trie_node_t;

// Idx is the index of divider using, ranging from 30 ~ 0
void insertToTrie(trie_node_t * node, int number, int idx) {
    if (idx < 0) {
        // reaching leaf
        node->number = number;
    } else {
        // Extract the bit
        int bit = !!(number & divider[idx]);
        if (! node->next[bit]) {
            // Never inserted before, malloc a new node
            node->next[bit] = malloc(sizeof(trie_node_t));
            node->next[bit]->next[0] = NULL;
            node->next[bit]->next[1] = NULL;
        }
        // Recursively insert the next one
        insertToTrie(node->next[bit], number, idx-1);
    }
}

// Search the trie and return the pair that has a max xor sum
// Same, idx goes from 30 to 0
int searchTrie(trie_node_t * left, trie_node_t * right, int idx) {
    if (!(left && right)) {
        // Bad combination
        return -1;
    } else if (idx < 0) {
        // Leaf node, get the final result for these two paths
        return left->number ^ right->number;
    } else {
        --idx;
        int l0r1 = searchTrie(left->next[0], right->next[1], idx);
        int l1r0 = searchTrie(left->next[1], right->next[0], idx);
        if (l0r1 != -1 || l1r0 != -1) {
            // If L0R1/L1R0 exist, the larger one among them must be the largest
            return l0r1 > l1r0 ? l0r1 : l1r0;
        }
        // L0R1/L1R0 does not exist, fall back to L0R0
        int l0r0 = searchTrie(left->next[0], right->next[0], idx);
        if (l0r0 != -1) {
            return l0r0;
        }
        // Final situation: L1R1
        return searchTrie(left->next[1], right->next[1], idx);
    }
}

int findMaximumXOR(int* nums, int numsSize){
    trie_node_t * root = malloc(sizeof(trie_node_t));
    root->next[0] = NULL;
    root->next[1] = NULL;

    for (int i = 0; i < numsSize; ++i) {
        insertToTrie(root, nums[i], 30);
    }

    return searchTrie(root, root, 30);
}

一个小优化

可以一次性分配一大块内存来存字典树的节点，比如用下面的 alloc_node() 替代 malloc(sizeof(trie_node_t)) ：

// Optimization: chunk allocator
// Max 2 * 10^5 numbers --> Max 2 * 32 * 10^5 nodes --> 2.5 * 10^4 chunks max
#define CHUNK_SIZE 256
trie_node_t * chunks[25000];
int alloc_idx = 0;

trie_node_t * alloc_node() {
    int chunk_idx = alloc_idx / CHUNK_SIZE;
    int chunk_offset = alloc_idx % CHUNK_SIZE;
    if (chunk_offset == 0) {
        chunks[chunk_idx] = malloc(CHUNK_SIZE * sizeof(trie_node_t));
    }
    ++alloc_idx;
    return chunks[chunk_idx] + chunk_offset;
}

这样可以减少内存分配次数，也能减少小块内存的分配开销（堆上对每块分配的内存的数据块头之类的）。LC的话是450ms减少到200ms左右，内存开销也从200M减少到了120M。